Many governments and academics around the world are calling for widespread or even universal testing for SARS-CoV-2, "the coronavirus."   Before endorsing, it's worthwhile becoming familiar with the clever stratagem of eighteenth-century Presbyterian minister Thomas Bayes.   It wouldn't be the first time his calculations will have come in handy: Alan Turing used Bayesian probabilities to help crack the Nazi Enigma Code.

Reverend Bayes died without knowing the value his statistical speculation would bring to the world — but people, examining posthumous notebooks, realized he'd discovered a fascinating trick of statistics.   Simply put, he calculated that the likelihood of an outcome's occurring depends on the background incidence of that outcome.   For example, is that potted palm real or fake?   Beware of being fooled by its lush green leaves; the likelihood that it contains chlorophyll instead of green dye depends on whether you're outdoors in Miami or in a corridor of a Chicago high rise.   The body of statistics Thomas Bayes wrapped around this phenomenon deservedly carries his name.

Bayes's Theorem stress-tests proposed coronavirus widespread-testing policy — yet outside data sciences, it's been nowhere mentioned during this crisis.   Since no diagnostic test can be 100% accurate, results are a probability game.   If you're in London or New York, the ensuing number of false COVID-19 diagnoses is inconvenient but relatively small.   But Bayes, peering through the centuries, demonstrates that the ratio of false results balloons when we extensively test symptomless people in communities with a low incidence of COVID-19.

Bayes's greatest import occurs twice: as populations enter into and leave coronavirus-active phases.   At those times of low disease prevalence, test imperfections are magnified, causing more "positive" tests than naïvely expected, bringing "false alarm" panics early on — and inappropriate delays to normalcy after the fact.

Why is that?    Although "a rose is a rose is a rose," not every positive is positively positive.   Modern laboratory tests carry "sensitivity" and "specificity" ratings of ~90–99%.   Sensitivity is "high" if the process finds nearly every truly sought object.   Specificity is the mirror ability to eliminate genuine negatives.   Societies value sensitivity over specificity — accepting, for instance, the TSA's occasionally mislabeling a harmless suitcase over allowing an actual bomb.

In peacetime, false triggers vastly outnumber true threats.    Similarly, the same coronavirus test has different meanings in different contexts.   To demonstrate, we're (briefly) going to be like the TSA, in two vastly different circumstances: wartime Baghdad, peacetime Kalamazoo.

Let's assume that our "sensitivity" is nearly perfect: every genuine device, we can positively identify as a bomb.   Our "specificity" isn't quite as high, because mundane electrical items have similar patterns, and bombs are designed to look mundane.   But, let's say we're pretty good: 95% of the time we think we've found one, we correctly identified it as real.   Conversely, 5% of items scanned are mistakenly deemed threats.

At a time in which Baghdad-bombs are fairly common (here 35% of total luggage), nearly all (87.5%) of our positive identifications will be accurate (Figure 1).

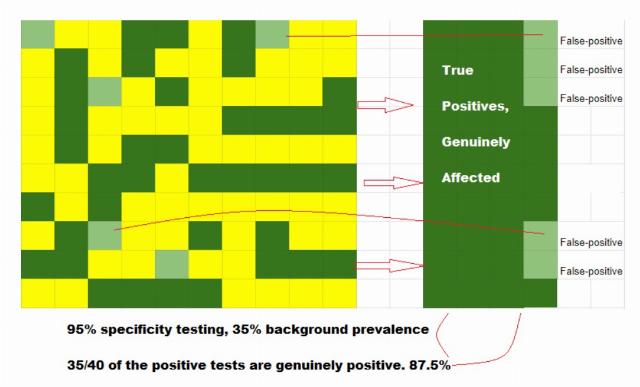
Figure 1: More true positives per false-positive test in high prevalence testing.

Conversely, a situation where only 1% of Kalamazoo-luggage is dangerous presents a far different scenario.   Searching 100 pieces, our "high sensitivity" finds the real one (~99% of the time) but (as before) mistakenly misidentifies as "real" 5% of general items (given our 95%- specificity).   With a low prevalence of devices, we wind up with the overwhelming majority of positive-IDs not the real deal (Figure 2).

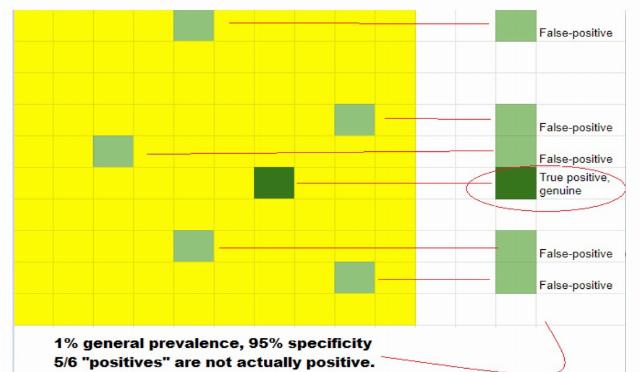
Figure 2: Fewer true positives per false-positive test in low-prevalence testing.

A Baghdad "positive" ID is almost always an actual threat; Kalamazoo's are nearly entirely false alarms.

Let's refocus on the coronavirus.   Imagine twin sisters testing COVID-19-positive.   Jean's a NYC front-line nurse; Jennifer's back home in rural Michigan.   Performing the same test on (essentially) the same person, merely at different locations, most everyone would assume that Jean and Jennifer equally likely corona-infected.

But, while coronavirus-epicenter NYC's prevalence rate approximates "Baghdad's," relatively untouched rural Michigan's is...well, Kalamazoo's.   Viewed through Bayes's prism, the same test's positive result nonetheless indicates to nearly the same level of certainty that Jean (Figure 1) has coronavirus infection and Jennifer (Figure 2) does not.   The two sisters can commiserate, but they should temper their expectations accordingly — and so should we.

A suspicious-suitcase's resolution is perfunctory and swift.   A "positive" coronavirus test's ramifications are upsetting and long-lasting — not just for the individual, but for families and neighborhoods, producing weeks of potentially unnecessary self-quarantine and cascading financial implications.

Universal testing, in the absence of a general likelihood of having the condition, entails havoc and upheaval in its indiscriminate wake.   The best testing is performed with and for other reasons.   Coronavirus testing is efficacious only where the disease is most likely to exist, and in those with documentable contact with active cases, or having symptoms themselves.

There's one other potential caveat on testing.   The coronavirus has been around as long as humans.   Less famous than SARS and COVID-19, other benign coronaviruses constitute ~18% of "common colds."   How many of those coronaviruses are floating around?    Does COVID-19 testing exclude their confounding presence?    The FDA won't approve tests unless this is the case, and companies so affirm — but every (pre-coronavirus) SARS test did cross-react with benign coronaviruses.   Additionally the determined accuracy levels emanate from closed-loop, reusable sample sets — not the general population.   Those percentage numbers are therefore unverified and frankly unverifiable in real time.

These factors are not commonly addressed during the calls for universal testing, yet they should be.   There's been enough confusion about numbers of cases without adding more.

Dr. Bock is a Yale University– and University of Rochester Medical School–trained primary care physician currently working in business development, biomedical devices, and angel investment.